CONTOH SOAL DAN PEMBAHASAN PROGRAM LINIER MATEMATIKA SMA

Assalamu'alaikum teman teman....
kali ini kita akan mempelajari tentang program linier matematika sma. materi ini memepelajari bagaimana mencari nilai maksimum/atau minimum dari suatu proses . oke, mari kita lihat pembahasannya.

soal pertama,,,
Tanah seluas 10.000 m² akan dibangun rumah tipe A dan tipe B. Untuk rumah tipe A diperlukan 100 m² dan tipe B diperlukan 75 m². Jumlah rumah yang dibangun paling banyak 125 unit. Keuntungan rumah tipe A adalah Rp 6.000.000,00/unit dan tipe B adalah Rp 4.000.000,00/unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah ........ 

jawaban,,,
misal:
x = rumah tipe A
y = rumah tipe B
100x + 75y ≤ 10.000 ⇒dibagi 25 --> 4x + 3y ≤ 400 …..(1)
x + y ≤ 125 …..(2)
Keuntungan maksimum : 6000.000 x + 4000.000 y =…?
Mencari keuntungan maksimum dengan mencari titik-titik pojok dengan menggunakan
sketsa grafik:
Grafik 1 :
4x + 3y ≤ 400
titik potong dengan sumbu X jika y=0 maka x =400/4= 100
Titik potongnya (100 , 0)
Titik potong dengan sumbu Y jika x = 0 maka y =400/3= 133,3
Titik potongnya (0 , 133,3)
Grafik 2 :
x + y ≤ 125
titik potong dengan sumbu X jika y=0 maka x = 125
Titik potongnya (125 , 0)
Titik potong dengan sumbu Y jika x = 0 maka y = 15 
Titik potongnya (0 , 125)
Gambar grafiknya:

tik potong :
eliminasi x
4x + 3y = 400 x 1 ⇒ 4x + 3y = 400
x + y = 125 x 4 ⇒     4x + 4y = 500 -
-y = -100
y = 100
x + y = 125
x = 125 - y
= 125 – 100 = 25 --> didapat titik potong (25, 100)
Titik pojok 6000.000 x + 4000.000 y
(100,0) 600.000.000
(0,125) 500.000.000
(25, 100) 150.000.000+ 400.000.000 = 550.000.000
Keuntungan maksimum adalah Rp.600.000.000


soal kedua,,,,
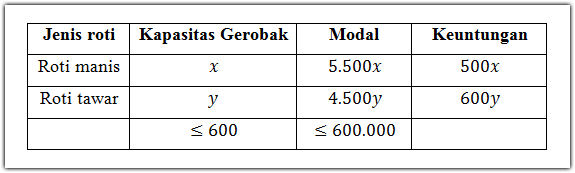
 Seorang pedagang menjual buah mangga dan pisang dengan menggunakan gerobak.
Pedagang tersebut membeli mangga dengan harga Rp. 8.000,00/kg dan pisang Rp.
6.000,00/kg. Modal yang tersedia Rp. 1200.000,00 dan gerobaknya hanya dapat
memuat mangga dan pisang sebanyak 180 kg. Jika harga jual mangga Rp.9200,00/kg
dan pisang Rp.7000,00/kg, maka laba maksimum yang diperoleh adalah…..

Jawab:
Misal : x = mangga ; y = pisang
Model matematikanya:
x ≥ 0 ; y≥ 0
8000x + 6000y ≤ 1200.000 --> dibagi 2000
⇔ 4x + 3y ≤ 600 ….(1)
x + y ≤ 180 ….(2)
Laba penjualan mangga = 9200 – 8000 = 1200
Laba penjualan pisang = 7000 – 6000 = 1000
Laba maksimum = 1200x + 1000y

maka grafiknya,,,

Titik potong:
Dari pers (1) dan (2)
eliminasi x
4x + 3y = 600 x1 ⇒ 4x + 3y = 600
x + y = 180 x4 ⇒ 4x + 4y = 720 -
- y = - 120
y = 120
x + y = 180
x = 180 – 120 = 60
titik potong = (60,120)

Titik pojok           1200x + 1000y
(0, 0)                              0
(150, 0)                      180.000
(60, 120)                    192.000
(0, 180)                       180.000
Laba maksimum adalah 192.000


untuk soal no 3,,,
Luas daerah parkir 1.760 m2. Luas rata – rata untuk mobil kecil 4 m2 dan mobil besar 20 m2. Daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil Rp.1.000,00/jam dan mobil besar Rp. 2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak kendaraan yang pergi dan datang, maka hasil maksimum tempat parkir itu adalah ….

jawabannya,,,
misal x = mobil kecil dan y = mobil besar, maka dapat dibuat persamaan sbb:
4 x + 20 y ≤ 1760 ⇒ x + 5 y ≤ 440 …(1)
x + y ≤ 200 …(2)
dari pers (1) dan (2)
eliminasi x
x + 5 y = 440
x +    y = 200 -
4 y = 240
y = 240/4
   = 60
x + y = 200
x + 60 = 200
x = 200 – 60 = 140
maka hasil maksimum
1000 x + 2000 y = 1000. 140 + 2000. 60 = 140000 + 120000 = Rp. 260.000,-


untuk pembahasan lebih lengkapnya,, silahkan klik tautan berikut ini,,,
download disini pembahasan program linier matematika sma

Read More

Belajar Materi Program LineAR

advertisements

Matematika ilmu yang tidak perlu kita buat sulit, karena matematika memang tidak sulit. Sebelumnya telah banyak materi matematika yang telah saya berikan artikelnya seperti invers fungsi, rumus pythagoras, statistika data tunggal dan statistika data kelompok, fungsi eksponen dan logaritma, dan masih banyak lagi yang lainnya. Kali ini topik yang akan kita bahas yaitu tentang program linear.

Program linear yaitu suatu metode untuk mencari nilai maksimum atau nilai minimum dari bentuk linear pada daerah yang dibatasi grafik -grafik fungsi linear.

Himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah merupakan suatu himpunan titik-titik (pasangan berurut (x,y)) dalam bidang cartesius yang memenuhi semua pertidaksamaan linear dalam sistem tersebut. Sehingga daerah himpunan penyelesaiannya merupakan irisan himpunan-himpunan penyelesaian dari pertidaksamaan dalam sistem pertidaksamaan linear dua peubah itu. Untuk  lebih mudah dalam memahami daerah penyelesaian dari sistem pertidak-samaan linear dua peubah, perhatikan contoh berikut.

Contoh:
Tentukan daerah  penyelesaian dari sistem pertidaksamaan linear berikut!
3x + 5y  15
x  0
y  0

Penyelesaian:
Gambar garis 3x + 5y =15, x = 0, dan y =0
Untuk 3x + 5y  15
Pilih titik (0,0), kemudian substitusikan ke pertidaksamaan sehingga diperoleh:
3 × 0 + 5× 0  15
0  15 (benar), artinya dipenuhi
Sehingga daerah penyelesaiannya adalah daerah yang memuat titik (0,0)
Untuk x  0, pilih titik (1,1) kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:
1  0 (benar), artinya dipenuhi.
Sehingga daerah penyelesaiannya adalah daerah yang memuat titik (1,1)
Untuk y  0, pilih titik (1,1) kemudian substitusikan ke pertidaksamaan sehingga diperoleh:
1  0 (benar), artinya dipenuhi.
Sehingga himpunan penyelesaiannya adalah daerah yang memuat titik (1,1).

Selanjutnya arsir daerah yang memenuhi persamaan, seperti gambar dibawah ini.

Daerah  penyelesaian sistem pertidaksamaan merupakan irisan dari ketiga himpunan penyelesaian pertidaksamaan di atas, yaitu seperti terlihat pada gambar berikut ini (daerah yang diarsir).

Pertidaksamaan Linear juga dapat digunakan untuk memecahkan masalah dalam kehidupan sehari-hari. Hal ini dapat dilakukan dengan memodelkan masalah menjadi model matematika. Jadi, Model matematika merupakan suatu cara sederhana untuk menerjemahkan suatu masalah ke dalam bahasa matematika dengan menggunakan persamaan, pertidaksamaan, atau fungsi.

Perhatikan contoh berikut :

Pak Adi merupakan seorang pedagang roti. Beliau menjual roti menggunakan gerobak yang dapat memuat 600 bungkus roti. Roti yang dijualnya yaitu roti manis dan roti tawar dengan harga masing-masing  Rp 5.500,00 untuk roti manis dan Rp 4.500,00 untuk roti tawar per bungkusnya. Dari penjualan roti tersebut, beliau memperoleh keuntungan Rp 500,00 dari sebungkus roti manis dan Rp 600,00 dari sebungkus roti tawar. Apabila modal yang dimiliki oleh Pak Budi adalah Rp 600.000, buatlah model matematika agar beliau dapat memperoleh keuntungan sebesar-besarnya!

Penyelesaian :

Permasalahan Pak Adi diatas  dapat dimodelkan dalam bentuk matematika dengan menggunakan sistem pertidaksamaan linear dua variabel. Dengan memisalkan banyaknya roti manis sebgai x dan roti tawar sebagai y sehingga diperoleh tabel sebagai berikut.

Berdasarkan tabel diatas jika kita tuliskan dalam bentuk pertidaksamaan linear menjadi

x + y ≤ 600,
5.500x + 4.500y ≤ 600.000,
Untuk x, y anggota bilangan cacah, x ≥ 0, y ≥ 0

Dua pertidaksamaan terakhir (baris ketiga) menunjukkan syarat dari nilai x dan y. Dikarena xdan y merupakan pernyataan yang menyatakan banyaknya roti, maka tidak mungkin nilai x dany bernilai negatif.

Perhatikan kolom keempat dari tabel di atas yang menyatakan fungsi yang akan ditentukan nilai maksimumnya (nilai optimum). Fungsi tersebut dapat dituliskan dalam persamaan matematika sebagai berikut.

f(x,y) = 500x + 600y

untuk menyelesaikan sistem pertidaksamaan diatas kita dapat mengikuti langkah berikut :

1. Ubah masalah tersebut ke dalam model matematika yaitu dengan membuat tabel, fungsi pembatas dan fungsi tujuan. Tabel di sini untuk mempermudah membaca data. Fungsi pembatas/kendala yaitu beberapa pertidaksamaan linier yang berhubungan dengan permasalahan tersebut. Fungsi tujuan/objektif yaitu suatu fungsi yang berhubungan dengan tujuan yang akan dicapai. Biasanya fungsi tujuan dinyatakan dengan f(x,y) = ax + by atau z = ax + by
2. Lukislah daerah penyelesaian dari fungsi pembatasnya
3. Tentukan koordinat-koordinat titik ujung daerah penyelesaian. Jika belum ada gunakan bantuan eliminasi dari perpotongan 2 garis
4. Ujilah masing-masing titik ujung daerah penyelesaian
5. Tentukan nilai terbesar/terkecilnya sesuai dengan tujuan yang akan dicapai

dimana langkah no 1 telah kita dapatkan karena disini rumus matematika menunjukan bagaimana cara membuat model matematika. Selanjutnya ikuti langkah berikutnya agar kita memperoleh daerah penyelesaiannya

Read More

Rumus program linier

Pertidaksamaan linier dengan ditentukan daerah penyelesaiannya

Sebelum kita membahas lebih lanjut kita harus mengetahui terlebih dahulu tentang perstidaksamaan linier dan juga cara menentukan daerah penyelsaian ( himpunan penyelesaian). Petidasamaan linier adalah kalimat terbuka yang menggunakan tanda <, >, , dan >

Read More